This is probably the last post in this series, at least until i find an interesting problem.
Magic square is an interesting one problem indeed. From wiki:
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same
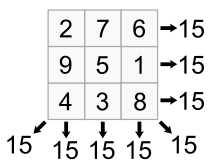
It’s interesting because constraints span across rows, columns and diagonals. So, I used the same technique as in the no-three-line problem but extending to diagonals(positive and negative) as well.
Starting with declarations
parameter SIZE=3;
rand int S;
rand int grid[SIZE][SIZE];
rand int gridt[SIZE][SIZE];
rand int diagp[SIZE];
rand int diagn[SIZE];
S variable is the sum. I initially put it down as 0:100 but i can force it with inline constraints anyway. The other constraints are for rows and columns which are the same as no-three-in-line.
constraint S_value{S inside {[0:100]};}
constraint grid_value { foreach(grid[i,j]) grid[i][j] inside {[0:S]}; }
constraint grid_row {foreach(grid[i]) grid[i].sum() == S;}
constraint gridt_value { foreach(gridt[i,j]) gridt[i][j] inside {[0:S]}; }
constraint gridt_row {foreach(gridt[i]) gridt[i].sum() == S;}
constraint cols {
foreach(grid[i, j]) {
grid[i][j] == gridt[j][i];
}
}
For positive diagonal, grid[i][i] works perfectly (well it is a square). for negative diagonal, grid[i][N-1-i] should works as well. as we move down rows, the negative diagonal move left from last column (N-1) to column 0.
constraint diagp_value { foreach(diagp[i]) diagp[i] inside {[0:S]};}
constraint diagp_row { diagp.sum() == S;}
constraint pdaig {
foreach(grid[i]) {
(grid[i][i] == diagp[i]);
}
}
constraint diagn_value { foreach(diagn[i]) diagn[i] inside {[0:S]};}
constraint diagn_row { diagn.sum() == S ;}
constraint ndaig {
foreach(grid[i]) {
(grid[i][SIZE-1-i] == diagn[i]);
}
}
Finally, S should be solved before other constraints(if i don’t use inline constraints). So, I am using solve before.
constraint sum_c {
solve S before grid;
solve S before gridt;
solve S before diagp;
solve S before diagn;
}
And the output for S=15 would be
2 7 6
9 5 1
4 3 8