DCT is frequency domain transform with cosine frequencies. Wiki says it all:
A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies
The equation to calculate g[u][v] DCT coefficients for 8x8 matrix (used for JPEG).
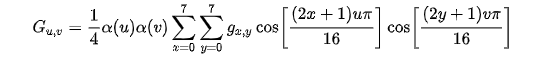
Brute force calculation can be done with next loops. It sure can be better with caching cosine multiplication or better butterfly implementation.
import math
mat = [
[-76, -73, -67, -62, -58, -67, -64, -55],
[-65, -69, -73, -38, -19, -43, -59, -56],
[-66, -69, -60, -15, 16, -24, -62, -55],
[-65, -70, -57, -6, 26, -22, -58, -59],
[-61, -67, -60, -24, -2, -40, -60, -58],
[-49, -63, -68, -58, -51, -60, -70, -53],
[-43, -57, -64, -69, -73, -67, -63, -45],
[-41, -49, -59, -60, -63, -52, -50, -34],
]
def A(idx):
r = 1.0/math.sqrt(2) if idx == 0 else 1.0
return r
def mydct(mat):
N = len(mat)
#Fuv = N * [ N * [0.0]]
Fuv = [
[-76, -73, -67, -62, -58, -67, -64, -55],
[-65, -69, -73, -38, -19, -43, -59, -56],
[-66, -69, -60, -15, 16, -24, -62, -55],
[-65, -70, -57, -6, 26, -22, -58, -59],
[-61, -67, -60, -24, -2, -40, -60, -58],
[-49, -63, -68, -58, -51, -60, -70, -53],
[-43, -57, -64, -69, -73, -67, -63, -45],
[-41, -49, -59, -60, -63, -52, -50, -34],
]
for i in range(N):
for j in range(N):
sum_ = 0
for x in range(N):
for y in range(N):
sum_ = sum_ + mat[x][y] * math.cos((2 * x + 1) * i * math.pi / (2 * N)) * math.cos((2 * y + 1) * j * math.pi / (2 * N))
Fuv[i][j] = (1/math.sqrt(2 * N)) * A(i) * A(j) * sum_
return Fuv
r = mydct(mat)
print(r)
The output coefficients are. Probably worth noting that first element ([0][0]) is called the DC coefficient which is the largest coefficient in the matrix.
[[-415.3749999999999, -30.185717276809033, -61.1970619502957, 27.23932249600452, 56.124999999999964, -20.095173772334842, -2.387647095293558, 0.46181544244846645], [4.4655237014136855, -21.857439332259844, -60.75803811653402, 10.253636818417837, 13.145110120476232, -7.0874180078452005, -8.535436712969494, 4.8768884966804045], [-46.834484742312476, 7.370597353426694, 77.12938757875553, -24.561982249733376, -28.911688429320662, 9.933520952775087, 5.416815472394543, -5.648950862137469], [-48.53496666553105, 12.068360940019197, 34.09976717271505, -14.759411080801929, -10.240606801750438, 6.295967438373016, 1.8311650530957317, 1.945936514864812], [12.12499999999995, -6.553449928892075, -13.196120970971862, -3.951427727907836, -1.8749999999999893, 1.7452844510267367, -2.7872282503369483, 3.1352823039767697], [-7.7347436775991625, 2.905461382890558, 2.379795764875581, -5.939313935865533, -2.37779670673259, 0.9413915961413784, 4.303713343622748, 1.8486910259091216], [-1.030674013497251, 0.18306744355204074, 0.41681547239454186, -2.4155613745353888, -0.8777939199423077, -3.0193065522845317, 4.120612421244484, -0.6619484539385858], [-0.16537560203663063, 0.14160712244184515, -1.0715363895103496, -4.192912078044711, -1.170314092006254, -0.09776107933753686, 0.5012693916445825, 1.6754588169203766]]