Wiki says that Percolation is

refers to the movement and filtering of fluids through porous materials

To put this in CS/Math terms:

Starting with N*N grid with and open and closed cells, is there a path from top row to bottom row?

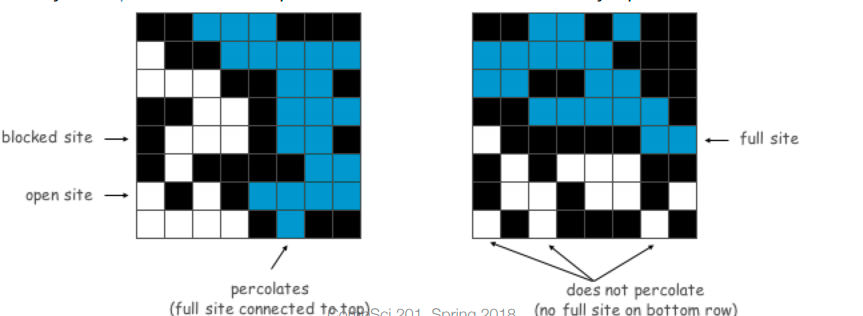
This is an example from link that shows how system percolates or not. Example image

Percolation is a problem that shows up in chemistry and physics. Also, in network connectivity or Maze connectivity. basically asking “is there a path between two points on grid”.

Union find Link to heading

one of the algorithms to solve the percolation system is converting the grid to union-find problem and check if the bottom and top nodes are connected.

The union find works by separating nodes into components. and defining operations that process these components.

union merges the components that contain nodes p,q. find returns the component containing the node p. connected checks if two nodes are in the same component.

    def union( p ,q):
    def find( p):
    def connected(p,q):

I did two implementation one for QuickFind with fast lookup but slow union. and QuickUnion which uses Fast union operation. that said, QuickUnion may show O(N) in worst case for both find and union.

class QuickFind():
    def __init__(self, N):
        self.N = N
        self.id = []
        for i in range(N):
            self.id.append(i)

    def union(self, p ,q):
        logging.info(f"UF: Connecting {p} and {q}")
        new_id = self.id[q]
        old_id = self.id[p]
        for i in range(self.N):
            if (self.id[i] == old_id):
                self.id[i] = new_id
    def find(self, p):
        return self.id[p]
    def connected(self,p,q):
        return self.find(p) == self.find(q)

class QuickUnion():
    def __init__(self, N):
        self.N = N
        self.id = []
        for i in range(N):
            self.id.append(i)

    def union(self, p ,q):
        logging.info(f"UF: Connecting {p} and {q}")
        self.id[self.find(p)] = self.find(q)
        logging.info(f"id={self.id}")
    def find(self, p):
        root = self.id[p]
        while (not root ==  self.id[root]):
            root = self.id[root]
        return root
    def connected(self,p,q):
        return self.find(p) == self.find(q)

Percolation Link to heading

I created UF with (N*N+2) nodes. the extra 2 notes are top and bottom notes. At the start, the first row is connected to top node and bottom row is connected to bottom row.

        self.TOP    = (N * N)
        self.BOTTOM = (N * N) + 1
        uf = QuickUnion((N*N)+2) # N*N nodes and 2 for top and bottom nodes
        # Connect top and bottom nodes
        for i in range(self.N):
            uf.union(xy_to_idx(0,   i,N), self.TOP)
            uf.union(xy_to_idx(N-1, i,N), self.BOTTOM)

the main loop starts opening cells in the grid and check if system percolates

    def open_site(self):
        # generate random cell and copen it
        idx = randrange(self.N * self.N)
        (x,y) = idx_to_xy(idx, self.N)

        if self.grid[x][y] == False:
            logging.info(f"Opening cell ({x},{y})")
            self.grid[x][y] = True
            
            # connect to surrouding cells
            for cell in neighbours(x,y,self.N):
                if self.grid[cell[0]][cell[1]] == True:
                    self.uf.union(xy_to_idx(x,y,self.N), xy_to_idx(cell[0], cell[1],self.N))

Side note, neighbours is utility created to get the neighbour cells taking into account the edges and corner

def isOnGrid(x,y,N):
    return (x >=0) and (y >=0) and (x < N) and (y < N)
def neighbours(x,y,N):
    l = []
    xx = 0
    for yy in [-1,1]:
        if isOnGrid(x + xx, y + yy,N):
            l.append((x+xx,y+yy))
    yy = 0
    for xx in [-1,1]:
        if isOnGrid(x + xx, y + yy,N):
            l.append((x+xx,y+yy))

Checking if system percolates is just asking if TOP and BOTTOM nodes are connected (ie in the same component).

    def is_perculatres(self):
        return self.uf.connected(self.TOP, self.BOTTOM)

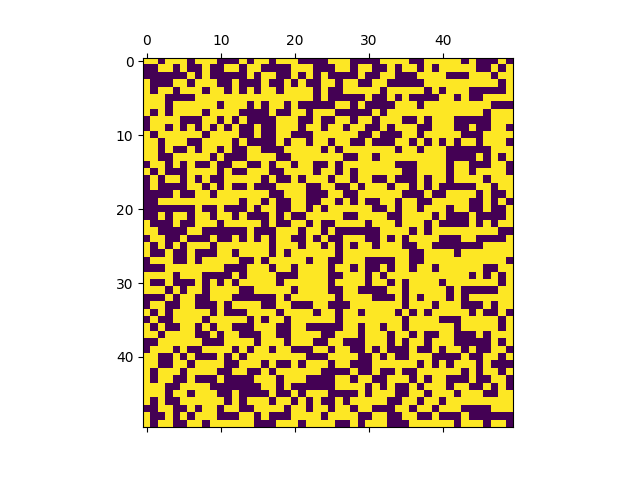
Finally, matplotlib is used to show the final grid for reference and calculate the percentage of opened cells.

WARNING:root:Percentage=0.5852

Example image